Презентация по алгебре 7 класс "Формулы сокращенного умножения". Формулы 7 класс алгебра
7 класс. Алгебра
Рубрика "7 класс. Алгебра"
I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.
Пример 1. Умножить одночлен на многочлен: 2a·(4a2-0,5ab+5a3).
Решение. Одночлен 2а будем умножать на каждый одночлен многочлена:
2a·(4a2-0,5ab+5a3)=2a∙4a2+2a∙(-0,5ab)+2a∙5a3=8a3-a2b+10a4. Запишем полученный многочлен в стандартном виде:
10a4+8a3-a2b.
Пример 2. Умножить многочлен на одночлен: (3xyz5-4,5x2y+6xy3+2,5y2z)∙(-0,4x3).
Решение. Каждое слагаемое, стоящее в скобках, умножаем на одночлен (-0,4x3).
(3xyz5-4,5x2y+6xy3+2,5y2z)∙(-0,4x3)=
=3xyz5∙(-0,4x3) -4,5x2y∙(-0,4x3)+6xy3∙(-0,4x3)+2,5y2z∙(-0,4x3)=
=-1,2x4yz5+1,8x5y-2,4x4y3-x3y2z.
II. Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.
III. Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.
Пример 3. Разложить на множители многочлен: 5a3+25ab-30a2.
Решение. Вынесем общий множитель всех членов многочлена за скобки. Это одночлен 5а, потому что на 5а делится каждый из членов данного многочлена. Итак, 5а мы запишем перед скобками, а в скобках запишем частные от деления каждого одночлена на 5а.
5a3+25ab-30a2=5a·(a2+5b-6a). Проверяем себя: если мы умножим 5а на многочлен в скобках a2+5b-6a, то получим данный многочлен 5a3+25ab-30a2.
Пример 4.Вынесите общий множитель за скобки: (x+2y)2-4·(x+2y).
Решение. (x+2y)2-4·(x+2y)=(x+2y)(x+2y-4).
Общим множителем здесь являлся двучлен (х+2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x+2y)2 и -4·(x+2y) на их общий делитель
(х+2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x+2y) и (x+2y-4), другими словами, мы разложили многочлен (x+2y)2-4·(x+2y) на множители. Ответ: (x+2y)(x+2y-4).
IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.
Пример 5. Выполнить умножение многочленов: (4x2-6xy+9y2)(2x+3y).
Решение. По правилу мы должны каждый член первого многочлена (4x2-6xy+9y2) умножить на каждый член второго многочлена (2x+3y). Чтобы не запутаться, делайте всегда так: сначала умножьте каждый член первого многочлена на 2х, потом опять каждый член первого многочлена умножайте на 3у.
(4x2-6xy+9y2)(2x+3y)=4x2∙2x-6xy∙2x+9y2∙2x+4x2∙3y-6xy∙3y+9y2∙3y=
=8x3-12x2y+18xy2+12x2y-18xy2+27y3=8x3+27y3.
Подобные слагаемые -12x2y и 12x2y, а также 18xy2 и -18xy2 оказались противоположными, их суммы равны нулю.
Ответ: 8x3+27y3.
I. Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.
Например, многочлен 2a+3a2b-6b4+3,5a3b состоит из суммы четырех одночленов.
II. Двучлен – это многочлен, состоящий из двух членов (одночленов).
Примеры двучленов: 2a-3b; 6x2+5; 2x-1.
III. Трехчлен – это многочлен, состоящий из трех членов (одночленов).
Например, 2а+3с-х или x2+4x-5 — трехчлены, так как состоят из трех одночленов.
IV. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.
Например, многочлен 2a2-3b+abc-d2 имеет третью степень, так как наибольшей степенью входящих в него одночленов является третья степень одночлена abc (складываем показатели: 1+1+1=3).
Многочлен 4x4yz+2x2y3-xz4+3x2y2 имеет шестую степень, так как наибольшей (шестой) степенью является степень его члена 4x4yz (складываем показатели: 4+1+1=6).
V. Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.
Например, приведенный выше многочлен 4x4yz+2x2y3-xz4+3x2y2 является многочленом стандартного вида, так как записан в порядке убывания степеней его членов.
Пример 1. Упростить многочлен, записав каждый его член в стандартном виде: 4aabb∙(-0,5c2)+5a2bb3-6abcab2c.
Решение.
4aabb∙(-0,5c2)+5a2bb3-6abcab2c=-2a2b2c2+5a2b4-6a2b3c2, а теперь запишем этот многочлен в стандартном виде (в порядке убывания степеней его членов):
-6a2b3c2-2a2b2c2+5a2b4.
Пример 2. Вычислить значение многочлена 5y2-3xy+x2при x=-1, y=2.
Решение.
5y2-3xy+x2=5∙22-3∙(-1)∙2+(-1)2=5∙4+6+1=27.
Пример 3. Упростить многочлен 2aba-a3bb+7bbbb и найти его числовое значение при a=3, b=2.
Решение.
Упрощаем многочлен: 2aba-a3bb+7bbbb=2a2b-a3b2+7b4.
Подставляем значения a и b.
2a2b-a3b2+7b4=2∙32∙2-33∙22+7∙24=2∙9∙2-27∙4+7∙16=36-108+112=40.
Пример 4. Привести подобные члены многочлена:
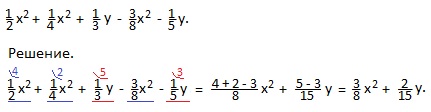
Пример 5. Привести к стандартному виду многочлен:
Напоминание: подобными считают одночлены, имеющие одинаковую буквенную часть.
I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.
Примеры одночленов:
а) a; б) ab; в) 12; г) -3c; д) 2a2∙(-3,5b)3; е) -123,45xy5z; ж) 8ac∙2,5a2∙(-3c3).
II. Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена.
Так, одночлены, приведенные выше, под буквами а), б), в), г) и е) записаны в стандартном виде, а одночлены под буквами д) и ж) требуется привести к стандартному виду, т. е. к такому виду, когда на первом месте стоит числовой множитель, а за ним записывают буквенные множители с их показателями, причем, буквенные множители стоят в алфавитном порядке. Приведем одночлены д) и ж) к стандартному виду.
д) 2a2∙(-3,5b)3=2a2∙(-3,5)3∙b3=-2a2∙3,5∙3,5∙3,5∙b3=-85,75a2b3;
ж) 8ac∙2,5a2∙(-3c3)=-8∙2,5∙3a3c3=-60a3c3.
III. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.
Примеры. Какую степень имеют одночлены а) — ж)?
а) a. Первую;
б) ab. Вторую: а в первой степени и b в первой степени-сумма показателей 1+1=2;
в) 12. Нулевую, так как буквенных множителей нет;
г) -3c. Первую;
д) -85,75a2b3. Пятую. Мы привели этот одночлен к стандартному виду, имеем а во второй степени и b в третьей. Складываем показатели: 2+3=5;
е) -123,45xy5z. Седьмую. Сложили показатели степеней буквенных множителей: 1+5+1=7;
ж) -60a3c3. Шестую, так как сумма показателей буквенных множителей 3+3=6.
IV. Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.
Пример. Указать подобные одночлены среди данных одночленов 1) -7).
1) 3aabbc; 2) -4,1a3bc; 3) 56a2b2c; 4) 98,7a2bac; 5) 10aaa2x; 6) -2,3a4x; 7) 34x2y.
Приведем одночлены 1), 4) и 5) к стандартному виду. Тогда строчка данных одночленов будет выглядеть так:
1) 3a2b2c; 2) -4,1a3bc; 3) 56a2b2c; 4) 98,7a3bc; 5) 10a4x; 6) -2,3a4x; 7) 34x2y.
Подобными будут те, которые имеют одинаковую буквенную часть, т.е. 1) и 3); 2) и 4); 5) и 6).
1) 3a2b2c и 3) 56a2b2c;
2) -4,1a3bc и 4) 98,7a3bc;
5) 10a4x и 6) -2,3a4x.
Очень большие и очень малые числа принято записывать в стандартном виде: a∙10n, где 1≤а<10 и n (натуральное или целое) – есть порядок числа, записанного в стандартном виде.
Например, 345,7=3,457∙102; 123456=1,23456∙105; 0,000345=3,45∙10-4.
Примеры.
Записать в стандартном виде число: 1) 40503; 2) 0,0023; 3) 876,1; 4) 0,0000067.
Решение.
1) 40503=4,0503·104;
2) 0,0023=2,3∙10-3;
3) 876,1=8,761∙102;
4) 0,0000067=6,7∙10-6.
Еще примеры на стандартный вид числа.
5) Число молекул газа в 1 см3 при 0°С и давлении 760 мм.рс.ст равно
27 000 000 000 000 000 000. Записать это число в стандартном виде.
Решение.
27 000 000 000 000 000 000=2,7∙1019.
6) 1 парсек (единица длины в астрономии) равен 30 800 000 000 000 км. Записать это число в стандартном виде.
Решение.
1 парсек=30 800 000 000 000=3,08∙1013 км.
В тему:
Киловатт-час — это внесистемная единица энергии или работы, применяется в электротехнике, обозначается кВт·ч.
1 кВт·ч=3,6∙106 Дж (Джоулей).
I. Определение. (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:
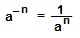
Примеры. Вычислить:
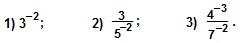
Решение.
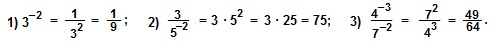
II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:
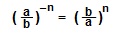
Примеры. Вычислить:
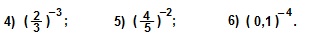
Решение.
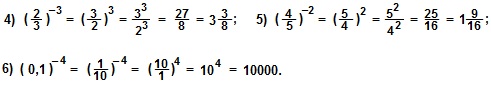
Свойства степени с натуральным показателем справедливы и для степеней с любым показателем.
Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.
Примеры на все свойства степени.
Упростить:
Решение.
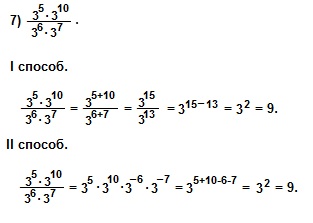При решении 7) примера I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями: am∙an=am+n и am:an=am-n. При решении II способом мы использовали понятие степени с отрицательным показателем: 
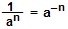и свойство произведения степеней с одинаковыми основаниями: am∙an=am+n .
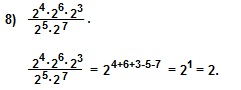Пример 8 ) решаем так же, как решали пример 7) вторым способом.
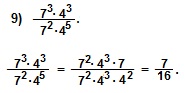
В примере 9) представим 73как 72∙7, а степень 45как 43∙42, а затем сократим дробь на (72∙43).
В 10) примере применим формулу степени произведения: (ab)n=an∙bn, а затем сократим дробь на (26∙35).
I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аn.
Примеры. Записать произведение в виде степени.
1) mmmm; 2) aaabb; 3) 5·5·5·5·ccc; 4) ppkk+pppk-ppkkk.
Решение.
1) mmmm=m4, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.
2) aaabb=a3b2; 3) 5·5·5·5·ccc=54c3; 4) ppkk+pppk-ppkkk=p2k2+p3k-p2k3.
II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аn – степень, а – основание степени, n – показатель степени. Например:
23 — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 23равно 8, так как 23=2·2·2=8.
Примеры. Написать следующие выражения без показателя степени.
5) 43; 6) a3b2c3; 7) a3-b3; 8 ) 2a4+3b2.
Решение.
5) 43=4·4·4; 6) a3b2c3=aaabbccc; 7) a3-b3=aaa-bbb; 8) 2a4+3b2=2aaaa+3bb.
III. а0=1 Любое число (кроме нуля) в нулевой степени равно единице. Например, 250=1. IV. а1=а Любое число в первой степени равно самому себе.
V. am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
Примеры. Упростить:
9) a·a3·a7; 10) b0+b2·b3; 11) c2·c0·c·c4.
Решение.
9) a·a3·a7=a1+3+7=a11; 10) b0+b2·b3=1+b2+3=1+b5;
11) c2·c0·c·c4=1·c2·c·c4=c2+1+4=c7.
VI. am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Примеры. Упростить:
12) a8:a3; 13) m11:m4; 14) 56:54.
12) a8:a3=a8-3=a5; 13) m11:m4=m11-4=m7; 14) 56:54=52=5·5=25.
VII. (am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают.
Примеры. Упростить:
15) (a3)4; 16) (c5)2.
15) (a3)4=a3·4=a12; 16) (c5)2=c5·2=c10.
Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:
15) (a3)4=(a4)3; 16) (c5)2=(c2)5.
VIII. (a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
Примеры. Упростить:
17) (2a2)5; 18) 0,26·56; 19) 0,252·402.
Решение.
17) (2a2)5=25·a2·5=32a10; 18) 0,26·56=(0,2·5)6=16=1;
19) 0,252·402=(0,25·40)2=102=100.
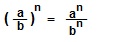IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
Примеры. Упростить:
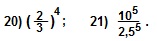
Решение.
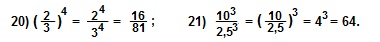
Функцию вида y=x3 называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x3 находятся в I и III четвертях.
Построение графика кубической функции y=x3
Составим таблицу значений функции y=x3 для х=0, х=±1, х=±2.
x | y=x3
0 | 0³=0 Точка О(0; 0)
1 | 1³=1 Точка А(1; 1)
-1 | (-1)³=-1 Точка С(-1; -1)
2 | 2³=8 Точка В(2; 8 )
-2 | (-2)³=-8 Точка D(-2; -8)
Функцию вида y=x2 называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x2 направлены вверх.
Построение графика функции y=x2. Составим таблицу значений функции для х=0, х=±1, х=±2, х=±3.
х | y=x²
0 | 0²=0
1 | 1²=1 Точка А(1; 1)
-1 | (-1)²=1 Точка А1(-1; 1)
2 | 2²=4 Точка В(2; 4)
-2 | (-2)²=4 Точка В1(-2; 4)
3 | 3²=9 Точка С(3; 9)
-3 | (-3)²=9 Точка С1(-3; 9)
data-ad-client="ca-pub-8602906481123293"data-ad-slot="2890988705"> 1) Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.(a+b)2 = a2+2ab+b2
a) (x + 2y)2 = x2 + 2 ·x·2y + (2y)2 = x2 + 4xy + 4y2
б) (2k + 3n)2 = (2k)2 + 2·2k·3n + (3n)2 = 4k2 + 12kn + 9n2
2) Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a-b)2 = a2-2ab+b2
а) (2a – c)2 = (2a)2-2·2a·c + c2 = 4a2 – 4ac + c2
б) (3a – 5b)2 = (3a)2-2·3a·5b + (5b)2 = 9a2 – 30ab + 25b2
3) Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.
a2–b2 = (a–b)(a+b)
a) 9x2 – 16y2 = (3x)2 – (4y)2 = (3x – 4y)(3x + 4y)
б) (6k – 5n)( 6k + 5n) = (6k)2 – (5n)2 = 36k2 – 25n2
4) Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a+b)3 = a3+3a2b+3ab2+b3
a) (m + 2n)3 = m3 + 3·m2·2n + 3·m·(2n)2 + (2n)3 = m3 + 6m2n + 12mn2 + 8n3
б) (3x + 2y)3 = (3x)3 + 3·(3x)2·2y + 3·3x·(2y)2 + (2y)3 = 27x3 + 54x2y + 36xy2 + 8y3
5) Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a-b)3 = a3-3a2b+3ab2-b3
а) (2x – y)3 = (2x)3-3·(2x)2·y + 3·2x·y2 – y3 = 8x3 – 12x2y + 6xy2 – y3
б) (x – 3n)3 = x3-3·x2·3n + 3·x·(3n)2 – (3n)3 = x3 – 9x2n + 27xn2 – 27n3
6) Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.
a3+b3 = (a+b)(a2–ab+b2)
a) 125 + 8x3 = 53 + (2x)3 = (5 + 2x)(52 — 5·2x + (2x)2) = (5 + 2x)(25 – 10x + 4x2)
б) (1 + 3m)(1 – 3m + 9m2) = 13 + (3m)3 = 1 + 27m3
7) Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.
a3-b3 = (a-b)(a2+ab+b2)
а) 64с3 – 8 = (4с)3 – 23 = (4с – 2)((4с)2 + 4с·2 + 22) = (4с – 2)(16с2 + 8с + 4)
б) (3a – 5b)(9a2 + 15ab + 25b2) = (3a)3 – (5b)3 = 27a3 – 125b3
Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.Страница 1 из 11
www.mathematics-repetition.com
| 1. |
Формула квадрата суммы или квадрата разности, проверка правильности использования формулы
Сложность: лёгкое |
1 |
| 2. |
Применение формулы разности квадратов
Сложность: лёгкое |
1 |
| 3. |
Формула квадрата суммы, возведение многочлена в квадрат
Сложность: лёгкое |
2 |
| 4. |
Формула разности квадратов
Сложность: лёгкое |
1 |
| 5. |
Формула квадрата разности
Сложность: лёгкое |
1 |
| 6. |
Формулы сокращённого умножения (формулировки)
Сложность: лёгкое |
1 |
| 7. |
Произведение разности и суммы (обыкновенные дроби)
Сложность: среднее |
3 |
| 8. |
Разность квадратов (степень)
Сложность: среднее |
3 |
| 9. |
Разность квадратов (десятичные дроби)
Сложность: среднее |
3 |
| 10. |
Произведение суммы и разности (целые числа)
Сложность: среднее |
3 |
| 11. |
Значение выражения
Сложность: среднее |
4 |
| 12. |
Квадрат суммы (десятичные дроби)
Сложность: среднее |
5 |
| 13. |
Квадрат разности (обыкновенные дроби)
Сложность: среднее |
5 |
| 14. |
Квадрат суммы (трином)
Сложность: среднее |
5 |
| 15. |
Квадрат разности (трином)
Сложность: среднее |
5 |
| 16. |
Разность кубов
Сложность: среднее |
5 |
| 17. |
Квадрат разности (умножение на число)
Сложность: среднее |
3 |
| 18. |
Произведение суммы двух чисел на неполный квадрат их разности
Сложность: сложное |
3 |
| 19. |
Формулы сокращенного умножения (десятичные дроби)
Сложность: сложное |
8 |
| 20. |
Разность квадратов (целые числа)
Сложность: сложное |
7 |
| 21. |
Произведение суммы и разности (числовое выражение)
Сложность: сложное |
5 |
www.yaklass.ru
Урок-зачет по алгебре по теме "Формулы сокращенного умножения" (7-й класс)
Разделы: Математика
Цели урока:
Образовательные: проверить уровень усвоения учащимися темы, знание ими соответствующих формул и правил.Развивающие: углубить знания учащихся, развить умения применять приемы сокращенного умножения при решении уравнений, при обнаружении и исправлении ошибок, объяснении своих действий, развитие творческой деятельности учащихся.Воспитательные: создание условий для включения каждого ученика в активную учебно-познавательную деятельность где каждый может проявить себя, воспитание интереса к математике, расширение кругозора, включение в урок исторического материала.
Тип урока: урок проверки, оценки и коррекции знаний, умений и навыков в форме путешествия « По стране формул». Задания подобраны по нарастающей степени сложности.
План путешествия:
1.«Лес правил» (игра «Домино»).
2. «Поляна соответствий» (верно установив соответствия ученик получает имя великого математика «Диофант», портрет, историческая справка).
3. «Озеро ошибок»
4. «Болото уравнений» (игра «Математическое поле чудес». Решив правильно уравнения, ученик выбирает ответы и переворачивает их. В результате получает имя великого математика «Эйлер», портрет, историческая справка).
5. «Остров формул» (творческое задание).
Каждый ученик получает маршрутный лист путешествия, на доске также написан план путешествия и формулы:
1.(a-b)²=a²-2ab+b² 2.(a+b)²=a²+2ab+b² 3.(a-b)(a+b)= a²-b² 4. a²-b²=(a-b)(a+b) 5.a³+b³=(a+b)(a²-ab+b²) 6. a³-b³=( a-b)(a²+ab+b²) 7. a²-2ab+b²=(a-b)² 8. a²+2ab+b²= (a+b)²
Ход урока:
Мотивационная часть. Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений. А сейчас мы начинаем наше путешествие и попадаем в лес правил.
1. Лес правил.
| Вопрос. Старт. Квадрат суммы двух выражений равен | Ответ. Финиш. Произведению суммы этих выражений и неполного квадрата их разности |
| Вопрос. Разность квадратов двух выражений равна | Ответ. Квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения |
| Вопрос. Квадрат разности двух выражений равен | Ответ. Произведению разности этих выражений и их суммы |
| Вопрос. Произведение разности двух выражений и их суммы равно | Ответ. Квадрату первого выражения, минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения |
| Вопрос. Сумма кубов двух выражений равна | Ответ. Разности квадратов этих выражений |
Разрезать на пять полосок и раздать ученикам. Начинает читать вопрос ученик, которому досталась карточка со словом «старт». Затем читает ответ второй ученик, у которого продолжение этой формулы, и он называет номер, под которым эта формула написана на доске, затем он зачитывает вопрос со своей карточки. Третий ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. Четвертый ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. Пятый ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. И заканчивает игру снова первый ученик. Ребята, мы успешно преодолели «Лес правил» и попали на «Поляну соответствий».
2. «Поляна соответствий»
| № формулы | формула | № ответа | ответ | буква |
| 1 | (x+3)² | 1 | 4x²-9 | О |
| 2 | x²-16 | 2 | 16x²-40xy+25y² | А |
| 3 | (2x-3)(2x+3) | 3 | (x-4)(x+4) | И |
| 4 | 81-18x+x² | 4 | (3y+6x)² | Т |
| 5 | (4x-5y)² | 5 | x²+6x+9 | Д |
| 6 | 25x²-49y² | 6 | (9-x)² | Ф |
| 7 | 9y²+36yx+36x² | 7 | (5x-7y)(5x+7y) | Н |
Каждый ученик получает карточку, выполняет задание, получает соответствия: 1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т).
Молодцы ребята, вы получили имя великого математика. Показываю его портрет. Историческая справка: Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время все алгебраические утверждения выражали в геометрической форме, вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
3. «Озеро ошибок»
Ученику нужно найти ошибку в каждой формуле и исправить ее на своих листах.
1.(4у-3х)(4у+3х)=8у²-9у² (вместо 8у² должно быть16у²) 2.100х²-4у²=(50х-2у)(50х+2у) (вместо50х должно быть10х) 3.(3х+у)²=9х²-6ху+у² (вместо-6ху должно быть+6ху) 4.(6a-9c)²=36a²-54ac+81c² (вместо-54ac должно быть-108ac) 5.х³+8=(х+2)(х²-4х+4) (вместо-4х должно быть-2х)
Затем вызываю учеников к доске исправить ошибки в примерах, они еще раз проговаривают формулы и правила. Ребята, мы преодолели «Озеро ошибок» и подошли к «Болоту уравнений».
4. «Болото уравнений»
1) х+х²+(5-х)(5+х)=26 2) (3х-4)(3х+4)=9х²-4х 3)(2+х)²-х²=24 4)(1-х)²-(3+х)²=-56 5)(2х-3)(2х+3)-х(4х-3)=15
Ученик получает пять квадратиков, на которых с одной стороны написаны цифры, а с другой стороны буквы. Правильно решив уравнения, ученик получает последовательность цифр, а перевернув их получает имя великого математика.
1 4 5 6 8 Э Й Л Е Р
Показываю его портрет. Даю историческую справку. Эйлер родился в 1707 году в Швейцарии. В 1727 году двадцатилетним юношей он был приглашен в Петербургскую Академию наук. Этот математик работал вместе с Ломоносовым. В Петербурге Эйлер получает возможность для создания и издания своих работ, их у него более 800 (72 тома). Среди его работ - первые учебники по решению уравнений. Старшеклассники учатся по учебникам, прообразы которых создал этот ученый. Его считают великим учителем математики. Последние 17 лет своей жизни он был слепым, но продолжал работать, диктовал труды своим ученикам. Ребята, мы не застряли в «Болоте уравнений» и перед нами «Остров формул».
5. «Остров формул»
1) b²+20b+*=(*+*)² 2)16m²-*= (*-8m)(*+8m) 3) (*+3x)²=49y²+*+* 4) (3a+*)(3a-*)=*-81 5) (5x-*)²=*-*+16
Ответы:
- b²+20b+100=(b+10)²
- 16m²-64n²=(4m-8n)(4m+8n)
- (7y+3x)²=49y²+42xy+9x²
- (3a+9)(3a-9)=9a²-81
- (5x-4)²=25x²-40x+16
Ученики должны восстановить формулы, заменив звездочки правильными выражениями. Затем вызываю учеников к доске, чтобы они восстановили правильное написание формул. Ученики еще раз проговаривают правила и объясняют свое решение.
Подвожу итог урока.
xn--i1abbnckbmcl9fb.xn--p1ai
Формулы сокращённого умножения - 7 класс - Алгебра - Каталог статей
Формулы сокращённого умноженияПри расчёте алгебраических многочленов для упрощения вычислений используются формулы сокращенного умножения. Всего таких формул семь. Их все необходимо знать наизусть.
Следует также помнить, что вместо a и b в формулах могут стоять как числа, так и любые другие алгебраические многочлены.
Разность квадратов
- Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
- a2 - b2 = (a - b)(a + b)
Примеры:• 152 - 22 = (15 - 2)(15 + 2) = 13 x 17 = 221• 9a2 - 4b2с2 = (3a - 2bc)(3a + 2bc)
Квадрат суммы
- Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа.
- (a + b)2 = a2 + 2ab + b2
Обратите внимание, что с помощью этой формулы сокращённого умножения легко находить квадраты больших чисел, не используя калькулятор или умножение в столбик.
Поясним на примере:Найти 1122.• Разложим 112 на сумму чисел, чьи квадраты мы хорошо помним.2 112 = 100 + 12• Запишем сумму чисел в скобки и поставим над скобками квадрат. 1122 = (100 + 12)2• Воспользуемся формулой квадрата суммы: 1122 = (100 + 12)2= 1002 + 2 x 100 x 12 + 122 = 10 000 + 2 400 + 144 = 12 544
Помните, что формула квадрат суммы также справедлива для любых алгебраических многочленов.• (8a + с)2= 64a2 + 16ac + c2
Предостережение!(a + b)2 не равно a2 + b2
Квадрат разности
- Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе плюс квадрат второго числа.
- (a - b)2 = a2 - 2ab + b2
Также стоит запомнить весьма полезное преобразование:(a - b)2 = (b - a)2
Формула выше доказывается простым раскрытием скобок:(a - b)2 = a2 - 2ab + b2 = b2 - 2ab + a2 = (b - a)2
Куб суммы
- Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
Запомнить эту «страшную» на вид формулу довольно просто.• Выучите, что в начале идёт a3.• Два многочлена посередине имеют коэффициенты 3.• Вспомним, что любое число в нулевой степени есть 1. (a0 = 1, b0= 1). Легко заметить, что в формуле идёт понижение степени a и увеличение степени b.
В этом можно убедиться: (a + b)3 = a3b0 + 3a2b1 + 3a1b2+ b3a0 = a3 + 3a2b + 3ab2 + b3
Предостережение!(a + b)3 не равно a3 + b3
Куб разности
- Куб разности двух чисел равен кубу первого числа минус утроенное произведение квадрата первого числа на второе плюс утроенное произведение первого числа на квадрат второго минус куб второго.
- (a - b)3 = a3 - 3a2b + 3ab2 - b3
Запоминается эта формула как и предыдущая, но только с учётом чередования знаков «+» и «-». Перед первым членом a3 стоит «+» (по правилам математики мы его не пишем). Значит, перед следующим членом будет стоять «-», затем опять «+» и т.д.(a - b)3 = + a3 - 3a2b + 3ab2 - b3 = a3 - 3a2b + 3ab2 - b3
Сумма кубовНе путать с кубом суммы!
- Сумма кубов равна произведению суммы двух чисел на неполный квадрат разности.
- a3 + b3 = (a + b)(a2 - ab + b2)
Сумма кубов - это произведение двух скобок.• Первая скобка - сумма двух чисел.• Вторая скобка - неполный квадрат разности чисел. Неполным квадратом разности называют выражение:
a2- ab + b2
Данный квадрат неполный, так как посередине вместо удвоенного произведения обычное произведение чисел.
Разность кубовНе путать с кубом разности!
- Разность кубов равна произведению разности двух чисел на неполный квадрат суммы.
- a3 - b3 = (a - b)(a2 + ab + b2)
Будьте внимательны при записи знаков.
Применение формул сокращенного умноженияСледует помнить, что все формулы, приведённые выше, используется также и справа налево.
Многие примеры в учебниках рассчитаны на то, что вы с помощью формул соберёте многочлен обратно.
Примеры:• a2+ 2a + 1 = (a + 1)2• (aс - 4b)(ac + 4b) = a2c2 - 16b2
matematik.3dn.ru
алгебра"Формулы сокращенного умножения " 7 класс
Открытый урок
По алгебре "Формулы сокращенного умножения"
(7-й класс)
Лохматова Т.А
Цели урока:
Образовательные: проверить уровень усвоения учащимися темы, знание ими соответствующих формул и правил.Развивающие: углубить знания учащихся, развить умения применять приемы сокращенного умножения при решении уравнений, при обнаружении и исправлении ошибок, объяснении своих действий, развитие творческой деятельности учащихся.Воспитательные: создание условий для включения каждого ученика в активную учебно-познавательную деятельность где каждый может проявить себя, воспитание интереса к математике, расширение кругозора, включение в урок исторического материала.
Тип урока: урок проверки, оценки и коррекции знаний, умений и навыков в форме путешествия « По стране формул». Задания подобраны по нарастающей степени сложности.
План путешествия:
1.«Лес правил» (игра «Домино»).
2. «Поляна соответствий» (верно установив соответствия ученик получает имя великого математика «Диофант», портрет, историческая справка).
3. «Озеро ошибок»
4. «Болото уравнений» (игра «Математическое поле чудес». Решив правильно уравнения, учениквыбирает ответы и переворачивает их. В результате получает имя великого математика «Эйлер»,портрет, историческая справка).
5. «Остров формул» (творческое задание).
Каждый ученик получает маршрутный лист путешествия, на доске также написан план путешествия и формулы:
1.(a-b)²=a²-2ab+b²2.(a+b)²=a²+2ab+b²3.(a-b)(a+b)= a²-b²4. a²-b²=(a-b)(a+b)5.a³+b³=(a+b)(a²-ab+b²)6. a³-b³=( a-b)(a²+ab+b²)7. a²-2ab+b²=(a-b)²8. a²+2ab+b²= (a+b)²
9.(a + b)3 = a3 + 3a2b + 3ab2 + b3
10.(a — b)3 = a3 — 3a2b + 3ab2 — b3
Ход урока:
Мотивационная часть.Ребята, формулы сокращенного умножения имеют широкое применение в математике, особенно в старших классах. Их используют при решении уравнений, раскрытии скобок, разложении многочленов на множители, нахождении значений выражений. Поэтому надо хорошо знать эти формулы и уметь применять их в преобразованиях выражений.А сейчас мы начинаем наше путешествие и попадаем в лес правил.
1. Лес правил.
Вопрос. Старт.Квадрат суммы двух выражений равен
Ответ. Финиш.Произведению суммы этих выражений и неполного квадрата их разности
Вопрос.Разность квадратов двух выражений равна
Ответ.Квадрату первого выражения, плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения
Вопрос.Квадрат разности двух выражений равен
Ответ.Произведению разности этих выражений и их суммы
Вопрос.Разность кубов двух выражений равна
Ответ.Квадрату первого выражения, минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения
Вопрос.Сумма кубов двух выражений равна
Ответ.Разности квадратов этих выражений
Разрезать на пять полосок и раздать ученикам. Начинает читать вопрос ученик, которому досталась карточка со словом «старт». Затем читает ответ второй ученик, у которого продолжение этой формулы, и он называет номер, под которым эта формула написана на доске, затем он зачитывает вопрос со своей карточки. Третий ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. Четвертый ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. Пятый ученик, которому досталось продолжение формулы, читает ответ, называет номер, под которым эта формула написана на доске и зачитывает вопрос со своей карточки. И заканчивает игру снова первый ученик. Ребята, мы успешно преодолели «Лес правил» и попали на «Поляну соответствий».
2. «Поляна соответствий»
№ формулы
формула
№ ответа
ответ
буква
1
(x+3)²
1
4x²-9
О
2
x²-16
2
16x²-40xy+25y²
А
3
(2x-3)(2x+3)
3
(x-4)(x+4)
И
4
81-18x+x²
4
(3y+6x)²
Т
5
(4x-5y)²
5
x²+6x+9
Д
6
25x²-49y²
6
(9-x)²
Ф
7
9y²+36yx+36x²
7
(5x-7y)(5x+7y)
Н
Каждый ученик получает карточку, выполняет задание, получает соответствия:1→5(Д), 2→3(И), 3→1(О), 4→6(Ф), 5→2(А), 6→7(Н), 7→4(Т).
Молодцы ребята, вы получили имя великого математика. Показываю его портрет.Историческая справка: Очень давно, в Древней Греции жили и работали замечательные ученые-математики, которые всю свою жизнь отдали служению науке. В то время все алгебраические утверждения выражали в геометрической форме, вместо сложения чисел говорили о сложении отрезков, а произведение двух чисел сравнивали с площадью, трех чисел-с объемом и т.д. первым ученым, который отказался от геометрических способов выражения и перешел к алгебраическим уравнениям был древнегреческий ученый-математик, живший в 3 веке до нашей эры Диофант. Появились формулы, которые стали называться формулами сокращенного умножения.
3. «Озеро ошибок»
Ученику нужно найти ошибку в каждой формуле и исправить ее на своих листах.
1.(4у-3х)(4у+3х)=8у²-9у² (вместо 8у² должно быть16у²)2.100х²-4у²=(50х-2у)(50х+2у) (вместо50х должно быть10х)3.(3х+у)²=9х²-6ху+у² (вместо-6ху должно быть+6ху)4.(6a-9c)²=36a²-54ac+81c² (вместо-54ac должно быть-108ac)5.х³+8=(х+2)(х²-4х+4) (вместо-4х должно быть-2х
6.(a-4)(a+4)=a2-4
7.(2x-y)(2x+y)=2x2-y2
8.(x+7)2=x2+49
9.(x+7)2=x2+7x+49
10.(3a-4b)2=9a2-24ab+16b2
Затем вызываю учеников к доске исправить ошибки в примерах, они еще раз проговаривают формулы и правила. Ребята, мы преодолели «Озеро ошибок» и подошли к «Острову формул».
Вариант 1.
1. Раскройте скобки: (5а – 2b)2
25a2 – 4b2
5a2 – 20ab + 2b2
25a2 – 10ab + 4b2
25a2 – 20ab + 4b2
2. Разложите на множители: х64 – 4у2
(х8 – 2у)(х8 + 2у)
(2у – х32)(2у + х32)
(2у + х32)(х32 – 2у)
(2у + х8)(2у – х8)
3. Раскройте скобки в выражении: (4х3 + 3у)(3у – 4х3)
16х6 – 9у2
9у2 – 16х6
9у2 – 16х9
16х9 – 9у2
Вариант 2.
1. Раскройте скобки: (а + 7b)2
a2 + 49b2
a2 + 14ab + 7b2
a2 + 14ab + 49b2
a2 + 7ab + 49b2
2. Разложите на множители: 16m2 – n16
(n8 – 4m)(n8 + 4m)
(4m – n4)(4m + n4)
(4m + n4)(n4 – 4m)
(4m + n8)(4m – n8)
3. Раскройте скобки в выражении: (5а5 + 2х)(2х – 5а5)
25а25 – 4х2
25а10 – 4х2
4х2 – 25а10
4х2 – 25а25
Подвожу итог урока.
1. Сегодня я узнал…
2. Было интересно..
3. Было трудно…
4. Я выполнил задание..
5. Теперь я могу..
6. Я приобрел…
7. Я научился..
8. Я понял, что..
9. У меня получилось…
10. Мне захотелось…
Теперь оцените себя сами. Выберете смайлик у себя на парте, на который вы сегодня поработали. Д/З
infourok.ru
Презентация по алгебре 7 класс "Формулы сокращенного умножения"
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда: Бурцева Елена Васильевна МАОУ СОШ №19 п.Пироговский
2 слайд
Описание слайда: Формулы сокращенного умножения
3 слайд
Описание слайда: Формулы сокращённого умножения 1) Квадрат суммы двух выражений 2) Квадрат разности двух выражений Разложение на множители (обратные формулы) 3) Разность квадратов двух выражений
4 слайд
Описание слайда: Формулы сокращённого умножения Разность кубов двух выражений Сумма кубов двух выражений Куб суммы двух выражений Куб разности двух выражений
5 слайд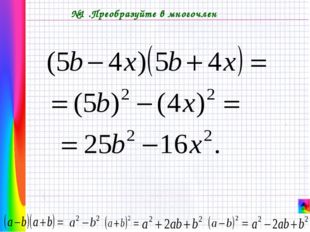
Описание слайда: №1 .Преобразуйте в многочлен
6 слайд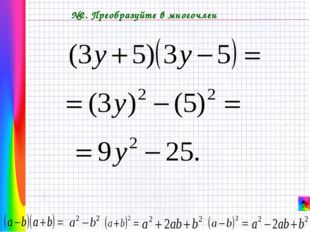
Описание слайда: №2. Преобразуйте в многочлен
7 слайд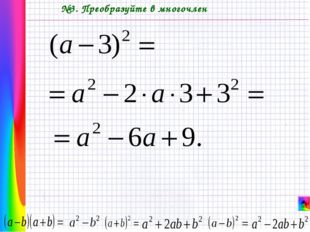
Описание слайда: №3. Преобразуйте в многочлен
8 слайд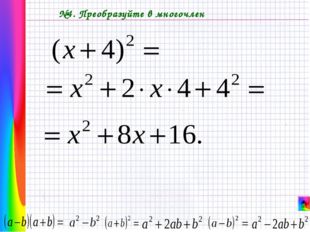
Описание слайда: №4. Преобразуйте в многочлен
9 слайд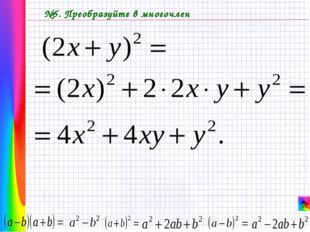
Описание слайда: №5. Преобразуйте в многочлен
10 слайд
Описание слайда: №6. Разложите на множители.
11 слайд
Описание слайда: №7. Разложите на множители.
12 слайд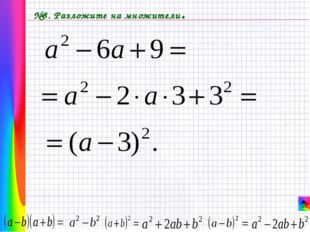
Описание слайда: №8. Разложите на множители.
13 слайд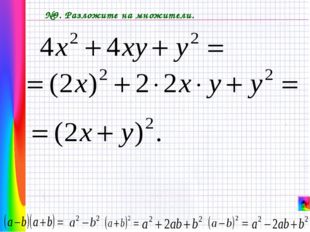
Описание слайда: №9. Разложите на множители.
14 слайд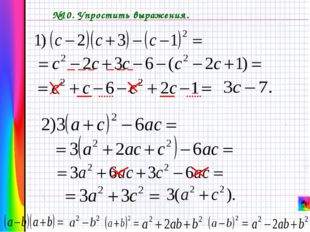
Описание слайда: №10. Упростить выражения.
15 слайд
Описание слайда: №1.Разложите на множители.
16 слайд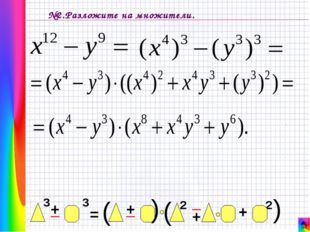
Описание слайда: №2.Разложите на множители.
17 слайд
Описание слайда: №3.Разложите на множители.
18 слайд
Описание слайда: №4.Разложите на множители.
19 слайд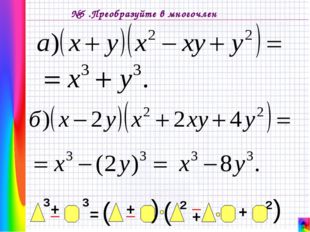
Описание слайда: №5 .Преобразуйте в многочлен
20 слайд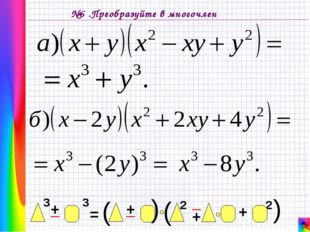
Описание слайда: №6 .Преобразуйте в многочлен
21 слайд
Описание слайда: Устно Представить в виде удвоенного произведения:
22 слайд
Описание слайда: Устно Представить в виде квадрата одночлена:
23 слайд
Описание слайда: Устно Представить в виде куба одночлена:
24 слайд
Описание слайда: Устно Разложить на множители:
25 слайд
Описание слайда: Устно Разложить на множители:
26 слайд
Описание слайда: Самостоятельная работа №1 1 вариант 2 вариант №1.Упростить выражение №2.Разложите на множители:
27 слайд
Описание слайда: Проверим №1: 1 вариант 2 вариант
28 слайд
Описание слайда: Проверим №2 (1 вариант)
29 слайд
Описание слайда: Проверим №2 (2 вариант)
30 слайд
Описание слайда: Самостоятельная работа №2 1 вариант 2 вариант Разложить на множители
31 слайд
Описание слайда: ПРОВЕРИМ! 1 вариант
32 слайд
Описание слайда: ПРОВЕРИМ! 2 вариант
33 слайд
Описание слайда: Самостоятельная работа №3 1 вариант 2 вариант №1.Выполните преобразование: №2.Выполните действия:
34 слайд
Описание слайда: Проверим №1: 1 вариант 2 вариант
35 слайд
Описание слайда: Проверим №2 (1 вариант)
36 слайд
Описание слайда: Проверим №2 (2 вариант)
37 слайд
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №352 Разложить на множители. Учебник Алимова Ш.А. и др.
38 слайд
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №353 Разложить на множители. Учебник Алимова Ш.А. и др.
39 слайд
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №356 Выполнить умножение. Учебник Алимова Ш.А. и др.
40 слайд
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №357 Выполнить умножение. Учебник Алимова Ш.А. и др.
41 слайд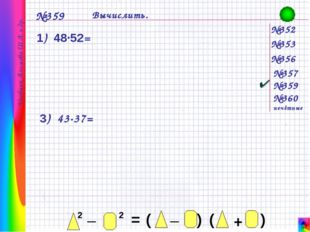
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №359 Вычислить. 1) 48·52= 3) 43·37= Учебник Алимова Ш.А. и др.
42 слайд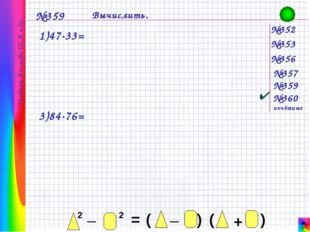
Описание слайда: №352 №353 №356 №357 №359 №360 нечётные №359 Вычислить. 1)47·33= 3)84·76= Учебник Алимова Ш.А. и др.
43 слайд
Описание слайда: №354 №355 №358 №361 №362 №354 нечётные Учебник Алимова Ш.А. и др. Разложить на множители.
44 слайд
Описание слайда: №354 №355 №358 №361 №362 №355 Учебник Алимова Ш.А. и др. нечётные Разложить на множители.
45 слайд
Описание слайда: №358 №354 №355 №358 №361 №362 Учебник Алимова Ш.А. и др. нечётные Выполнить умножение.
46 слайд
Описание слайда: №354 №355 №358 №361 №362 №361 Учебник Алимова Ш.А. и др. нечётные Разложить на множители.
47 слайд
Описание слайда: №354 №355 №358 №361 №362 №362 Учебник Алимова Ш.А. и др. нечётные Разложить на множители.
48 слайд
Описание слайда: №363(1,3,5) Вычислить: Учебник Алимова Ш.А. и др. №363 №365 №364 №366 №367 №368 нечётные №363 №366 №367 №368 нечётные
49 слайд
Описание слайда: Учебник Алимова Ш.А. и др. №364(1,3) Решить уравнения: №365 №364 №363 №366 №367 №368 нечётные
50 слайд
Описание слайда: Учебник Алимова Ш.А. и др. №365(1,3) Выполнить умножение: №365 №364 №363 №366 №367 №368 нечётные
51 слайд
Описание слайда: Учебник Алимова Ш.А. и др. №366(1,3) Вычислить: №365 №364 №363 №366 №367 №368 нечётные
52 слайд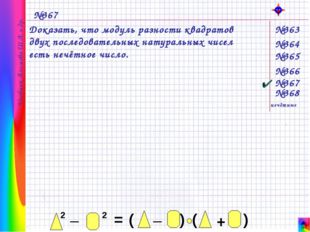
Описание слайда: Учебник Алимова Ш.А. и др. №367 Доказать, что модуль разности квадратов двух последовательных натуральных чисел есть нечётное число. №365 №364 №363 №366 №367 №368 нечётные
53 слайд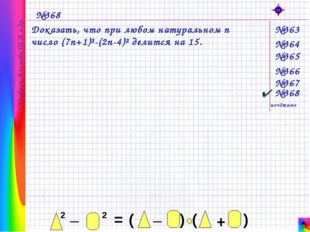
Описание слайда: Учебник Алимова Ш.А. и др. №368 Доказать, что при любом натуральном n число (7n+1)²-(2n-4)² делится на 15. №365 №364 №363 №366 №367 №368 нечётные
54 слайд
Описание слайда: №370(1,3) Представить квадрат двучлена в виде многочлена №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3)
55 слайд
Описание слайда: №371(1,3) Представить квадрат двучлена в виде многочлена №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3)
56 слайд
Описание слайда: №372(1,3) Представить квадрат двучлена в виде многочлена №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3)
57 слайд
Описание слайда: №373(1,3) Представить квадрат двучлена в виде многочлена №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3)
58 слайд
Описание слайда: №374(1,3) Выполнить действия, используя ФСУ №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3)
59 слайд
Описание слайда: №375(1,3) №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(1,3) №375(1,3) Выполнить действия, используя ФСУ
60 слайд
Описание слайда: №376(неч.) Применяя формулу (1+a)²≈1+2a, найти приближённое значение числа. №370(1,3) Учебник Алимова Ш.А. и др. №371(1,3) №372(1,3) №373(1,3) №374(1,3) №376(неч.) №375(1,3)
61 слайд
Описание слайда: №383(2,4) Разложить на множители: №383(2,4) №385(2,4) №384(2,4) №388(2,4) №416(2,4) №417(2,4) Учебник Алимова Ш.А. и др.
62 слайд
Описание слайда: №384(2,4) Решить уравнения: №383(2,4) №385(2,4) №384(2,4) №388(2,4) №416(2,4) №417(2,4) Учебник Алимова Ш.А. и др.
63 слайд
Описание слайда: №388(2,4) №385(2,4) №416(2,4) №417(2,4) Упростить выражения: №383(2,4) №384(2,4) №385(2,4) Учебник Алимова Ш.А. и др.
64 слайд
Описание слайда: №385(2,4) №384(2,4) №388(2,4) №388(2,4) №416(2,4) №417(2,4) Вычислить: №383(2,4) Учебник Алимова Ш.А. и др.
65 слайд
Описание слайда: №383(2,4) №385(2,4) №384(2,4) №388(2,4) №416(2,4) №416(2,4) №417(2,4) Упростить выражения: Учебник Алимова Ш.А. и др.
66 слайд
Описание слайда: №383(2,4) №385(2,4) №384(2,4) №388(2,4) №417(2,4) №416(2,4) №417(2,4) Решить уравнения: Учебник Алимова Ш.А. и др.
67 слайд
Описание слайда: №395(2,4) №396(2,4,6) №397(2,4) №398(2,4) №395(2,4) Разложить на множители Учебник Алимова Ш.А. и др.
68 слайд
Описание слайда: №396(2,4,6) Разложить на множители №395(2,4) №396(2,4,6) №397(2,4) №398(2,4) Учебник Алимова Ш.А. и др.
69 слайд
Описание слайда: №397(2,4) Вычислить. №395(2,4) №396(2,4,6) №397(2,4) №398(2,4) Учебник Алимова Ш.А. и др.
70 слайд
Описание слайда: №398(2,4) Вычислить. №395(2,4) №396(2,4,6) №397(2,4) №398(2,4) Учебник Алимова Ш.А. и др.
Найдите материал к любому уроку,указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Краткое описание документа:
Данная презентация представляет собой анимированные слайды для работы с интерактивной доской. В ней представлен материал для закрепления темы "Формулы сокращенного умножения" (алгебра 7 класс). Может использоваться для фронтальной и индивидуальной работы на уроках алгебры по учебникам, входящим в состав любых УМК..
Общая информация
Номер материала: ДA-025461
Похожие материалы
Оставьте свой комментарийinfourok.ru
Алгебра 7-9 классы. 7. Формулы сокращенного умножения
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание - как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Астрономия
- Обществознание
- Иностранные языки
- Технические науки
- Естествознание
forkettle.ru
